Сегодня мы с вами поговорим о том, как найти площадь равнобедренного треугольника. Ведь это может понадобиться как студентам и школьникам, так и другим людям. В данной статье вы узнаете формулы и хитрости, с помощью которых можно найти площадь равнобедренного треугольника. Итак, поехали!
Содержание:
Как найти площадь равнобедренного треугольника
Давайте сначала освежим в памяти, что же такое равнобедренный треугольник? Это фигура, имеющая три угла и три стороны, две из которых имеют одинаковую длину.
Для нахождения площади равнобедренного треугольника достаточно знать длину его основания, и высоту. Если мы их знаем, то достаточно перемножить эти две величины. После чего, необходимо произведение этих двух величин разделить на два.
Чаще всего, в задачах школьной программы, какая-то из этих необходимых составляющих нам неизвестна. Давайте разберёмся более подробно с каждым из таких случаев.
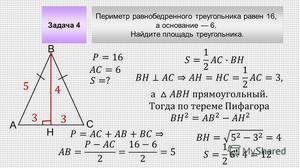
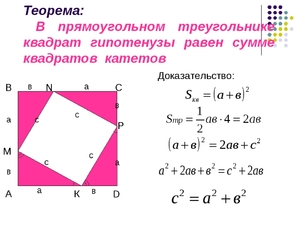
Допустим, что нам неизвестна высота. Но нам известны длины всех сторон треугольника. Для нахождения высоты нам необходимо воспользоваться теоремой Пифагора. А именно извлечь квадратный корень из разности квадратов боковой стороны и половины основания. Когда высота станет нам известной, мы можем смело пользоваться формулой, о которой только что говорили выше.
Этот вариант чисто логический. До этого может додуматься далеко не каждый школьник. Да что уж греха таить, даже не каждый взрослый. Поэтому для того, чтобы не ломать голову, существует специальная формула для такого случая. Необходимо перемножить сумму и разность между боковой стороной и половиной основания. После чего, извлечь из этого произведения квадратный корень. А потом, получившийся результат умножить на половину основания. Теперь давайте поговорим о других возможных вариантах нахождения площади равнобедренного треугольника.
Варианты нахождения площади равнобедренного треугольника
Сейчас мы рассмотрим возможные варианты школьных задач, где требуется определить площадь, и расскажем как их решать:
- Зная боковые стороны, и угол между ними. Для решения такой задачи необходимо длину боковой стороны возвести в квадрат, и разделить на два. После чего, следует умножить получившийся результат на синус угла между боковыми сторонами. В чём смысл? А в том, что если мы опустим высоту на боковую сторону равнобедренного треугольника, то её длина будет равна произведению длины основания на синус угла между боковыми сторонами. Далее, когда мы разделим пополам произведение длины боковой стороны и высоты, то вычислим значение площади равнобедренного треугольника.
- Зная боковую сторону, основание и угол при вершине. Для решения этой задачи необходимо перемножить длину боковой стороны на основание. После чего, нужно получившийся результат умножить на синус угла при основании, и разделить на два. Если сейчас подробно описывать как все получилось, то можно легко сбиться с толку. Поэтому здесь есть маленькая хитрость. Необходимо запомнить: произведение длины боковой стороны на синус угла при основании даёт нам значение высоты, опущенной на основание. Зная угол при вершине, мы можем легко найти угол при основании. Вот и все. Далее, зная длину основания и высоту, мы можем легко посчитать площадь.
- Зная основание и угол при нём. Эту задачу можно решить по довольно сложной формуле. Если формулы, которые вы могли прочитать выше ещё можно как-то вывести самому, то здесь её придётся просто запомнить. На всякий случай мы вам объясним почему эта формула именно такая. Если вы, или ваш ребёнок это поймёт, будет очень хорошо.
Итак, вначале необходимо найти тангенс половины угла при вершине. Найти его мы можем, зная угол при основании. После того, как вы нашли этот тангенс, необходимо разделить квадрат основания на 4 тангенса, полученного угла. Полученный результат и будет являться площадью нашего равнобедренного треугольника.
А теперь мы вам объясним, как все получается. Основной момент — это понять и заметить, что произведение половины основания на тангенс половины угла при вершине даёт нам высоту треугольника, опущенную на основание. Когда мы перемножим значение этой высоты на основание, и разделим пополам, то определим площадь. Формула даётся именно в таком виде, чтобы расчёт производился одним коротким действием, вместо длительных расчётов.
Кстати, треугольник, у которого все стороны равны тоже считается равнобедренным. Его площадь определить очень легко. Высота ищется по теореме Пифагора, после чего умножается на длину основания, и делится на два.
Дополнительные рекомендации
Чтобы научиться быстро решать подобные задачи, необходимо делать следующее:
- Постоянно тренироваться в решении подобных задач.
- Пробовать выучить формулы.
- Решать головоломки. Это поможет развить логическое мышление, и возможно придумать свой вариант решения задачи.
Взрослым также не рекомендуется забывать эти формулы. Иногда они пригождаются в реальной жизни при выполнении, например, ремонтных или хозяйственных работ.
Теперь вы знаете, как можно легко и просто найти площадь равнобедренного треугольника. В случае чего, вы можете помочь вашему ребёнку разобраться с этой темой, или решить домашнее задание.
Школьная геометрия — это очень легко. Поэтому рекомендуется посвятить два вечера решению большого количества подобных задач, и тогда, ваш ребёнок сможет решать их очень быстро.
Видео
В нашем видео вы найдете решение интересных задач о равнобедренных треугольниках.