Школа — это необъятная чаша знаний, которая включает в себя множество дисциплин, которые могут заинтересовать любого ребенка. Математика — царица точных наук. Строгая и дисциплинированная, она не терпит неточностей. Даже повзрослев, в обычной жизни мы можем столкнуться с разными математическими проблемами: вычисление квадратных метров для укладки плитки в ванной, кубических метров для определения объема бака и т. д., чего уж говорить о школьниках, которые только-только начинают свой математический путь.

Очень часто, начав изучать математику, точнее, геометрию, ученики путают плоские фигуры с объемными. Куб называют квадратом, шар — кругом, параллелепипед обычным прямоугольником. И здесь есть свои тонкости.
Сложно помочь ребенку в выполнении домашнего задания, не зная точно, объем или площадь какой фигуры — плоской или же объемной, нужно найти. Невозможно найти объем плоских фигур, таких как квадрат, круг, прямоугольник. В их случае можно найти лишь площадь. Прежде чем переходить к выполнению задачи, следует подготовить нужные атрибуты:
- Линейка, для того чтобы измерить необходимые нам данные.
- Калькулятор, для того чтобы в дальнейшем подсчитать расчеты.
Вычисление объема прямоугольного параллелепипеда
Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.
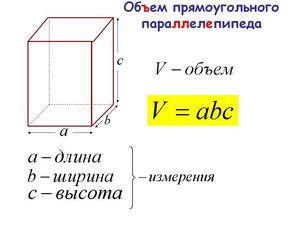
Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм. Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.
Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.
- После прочтения задачи, нужно определить что именно следует найти; длину фигуры, объем или же площадь.
- Какая именно часть фигуры рассматривается в задаче — ребро, вершина, грань, сторона, а может быть, вся фигура целиком?
Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:
V=a*b*h,
V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.
Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах.
Пример первый
Определим объем бака для спирта, при следующих размерах:
- длина три метра;
- ширина два метра пятьдесят сантиметров;
- высота триста сантиметров.
Для начала обязательно согласовываем единицы измерения и перемножаем их:
3*2.5*3.
Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.
Пример второй
Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.
Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.
Итак, начнем с сантиметров. Переводим метры в сантиметры:
V = 400 * 70 * 80;
V = 2240000 сантиметров в кубе.
Теперь метры:
V = 4* 0.7 * 0.8;
V = 2.24 метра в кубе.
Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.
Пример третий
Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:
V = a * b * h;
где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5
Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:
V = 5 * 3 * 2.5;
V = 37.5 метра в кубе.
Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.