Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Содержание:
Как составлять уравнение касательной в заданной точке
При написании уравнения будем использовать следующие обозначения:
- x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
- f(x) — исходная функция;
- f'(x) — производная от функции;
- k — угловой коэффициент.
Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.

Алгоритм написания уравнения
После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:
- Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
- Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
- Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
- Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.
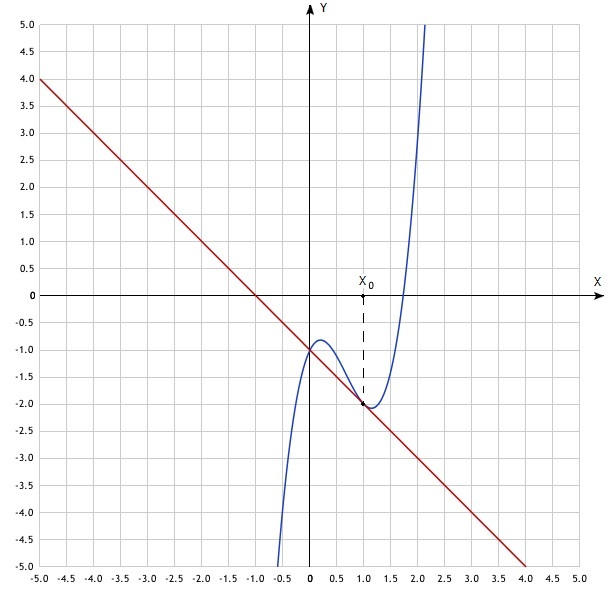
В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.
Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.
Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.
Задачи на написание уравнения касательной
Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.
Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.
Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.
- Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
- Возьмем от функции производную: f'(x) = 4x.
- Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
- Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
- Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.
В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.
Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).
- Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
- Запишем производную: g'(x) = 6x².
- Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
- Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
- Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
- В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.
Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.
Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.
Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.
Видео
Закрепить это тему вам поможет видео.