Чтобы вычислить пределы функции алгебраически, вы можете выбрать один из четырех методов: включение значения x, факторинг, рационализация числителя и поиск самого низкого общего знаменателя. Лучшим выбором является первый метод. Вы можете использовать эту технику только в том случае, если f непрерывна по значению x, в котором вы принимаете ограничение. Если f при этом не определена в значении х, вы должны перейти к другим методам, чтобы упростить вашу функцию и найти приблизительное значение для х.

Включение значения x
Первым методом алгебраического решения для нахождения f (x) является включение числа, в котором х приближается к функции. Если вы получаете неопределенное значение (0 в знаменателе или бесконечность), вы должны стремиться перейти к другому методу. Но если ваша f при этом непрерывна в значении х, вы получите значение, и все готово — вы нашли решение! Например, с помощью этого метода вы можете найти:
![]()
Пределом будет 3, так как f (5) = 3, и эта f непрерывна при х
Факторинг
Факторинг — это метод, который следует попробовать при сбое в подключении — особенно когда любая часть данной функции является полиномиальным выражением.
Если нужно выполнить это задание:
![]()
то сначала попробуйте подключить 4 к функции, и вы получите 0 в числителе и знаменателе, который говорит вам перейти к следующему методу. Квадратичное выражение в числителе говорит, чтобы вы попытались разложить его. Заметим, что числитель предыдущей функции имеет значение (х— 4) ( x — 2). Х — 4 отменяет на верхней и нижней части фракции. Этот шаг оставляет вас с f (х) = х— 2. Вы можете подключить 4 к этой непрерывной функции, чтобы получить 2.
Если вы нарисуете эту функцию, она выглядит как прямая f ( x ) = x — 2, но она имеет отверстие при x = 4, потому что исходная f все еще не определена (потому что она создает 0 в знаменателе). Эта цифра иллюстрирует это.
Если после того как вы учли верхнюю и нижнюю части дроби, термин в знаменателе не сократилось и значение, которое вы ищете не определен, f при этом значении x не существует (который вы можете написать как DNE ).
Например, эта f действует как показано:
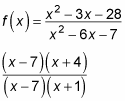
(Х — 7) сверху и снизу сократятся. Поэтому, если вас попросят найти функцию, когда x подходит 7, вы можете подключить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти

лимит DNE, потому что вы получите 0 в знаменателе. Следовательно, эта f имеет предельность где угодно, кроме как x приближается к -1.
Рационализация числителя
Третий метод требует, чтобы вы рационализировали числитель. Функции, требующие этого метода, имеют квадратный корень в числителе и полиномиальное выражение в знаменателе. Например, скажем, вас попросят вычислить предел этой функции по мере приближения x к 13:
![]()
Забивание номеров не получается, когда вы получаете 0 в знаменателе дроби. Факторинг терпит неудачу, потому что уравнение не имеет полиномиального фактора. В этой ситуации, если вы умножаете числитель и знаменатель на сопряжение числителя, термин в знаменателе, который был проблемой, отменяется, и вы сможете вычислить пределы:
-
Умножьте верхнюю и нижнюю части дроби конъюгатом.
Конъюгатом числителя является

Умножая, вы получаете эту настройку:
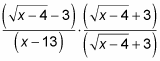
ИЗОБРАЖИТЕ числитель, чтобы получить

который упрощается до x — 13 (средние два члена отменяют, и вы объединяете как условия из FOIL).
-
Отменить факторы.
Отмена дает вам следующее выражение:
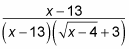
Условия ( x — 13) отменяются, оставляя вас с таким результатом:
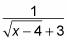
-
Вычислите пределы.
Когда вы вставляете 13 в функцию, вы получаете 1/6, что является пределом.
Самый низкий общий знаменатель
Когда вам дается сложная рациональная f, вы используете четвертую и окончательную алгебраическую методику определения пределов. Техника подключения не работает, потому что вы получаете 0 в одном из знаменателей. Функция не факторизуема, и у вас нет квадратных корней для рационализации. Поэтому вы можете перейти к последней технике. С помощью этого метода вы комбинируете функции, найдя наименьший общий знаменатель (LCD). Термины отменяются, и в этот момент вы можете найти предельность.
Например, выполните следующие действия, чтобы найти ограничение:
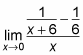
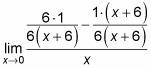
Распределите числители сверху.
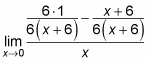
Добавьте или вычтите числители, а затем отмените условия.
Вычитание числителей дает вам
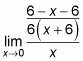
который затем упрощает
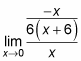
-
Используйте правила для фракций для дальнейшего упрощения.
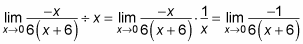
-
Замените предельное значение на эту функцию и упростите.
Для нахождения предела необходимо, когда x приближается к 0, поэтому здесь будет равен -1/36.
Вот и все методы с подробным описанием — надеюсь, теперь вы поняли, как решать пределы.
Видео
Этот видеоурок поможет вам лучше разобраться в материале, изложенном в статье и запомнить его.