В программировании, кроме общепринятой десятичной системы, работают с двумя дополнительными способами записи чисел: двоичной, восьмеричной, шестнадцатеричной. Каждый из видов относится к позиционному способу счисления. Он подразумевает присвоение неодинаковых значений каждому числовому знаку записи в зависимости от его расположения. Также существует позиционный тип и смешанный, но их сфера применения далека от программирования.
Содержание:
Общее представление о системах исчисления
Перевод одного типа в другой происходит по определенным алгоритмам. Каждый имеет свои преимущества и предназначен для разных целей. Двоичная система используется непосредственно самим компьютером в качестве простейшего представления данных. С помощью двух цифр 0 и 1 машина способна читать и обрабатывать любую информацию. Таким образом, число 100 будет выглядеть как сочетание цифр 1100100, а 1000 - 1111101000.
Шестнадцатеричная система подразумевает использование десяти цифр, а также первые 8 букв латинского алфавита. Шестнадцатеричная система кодирует не только числовые значения, но также текстовую информацию. Поэтому применяется для записей кодов ошибок системы или приложений, написания программ на низкоуровневых языках, таких как Java и Microsoft.NET. Таким образом, 1000 выглядит, как 3E8, а слово "число" будет представлено, как 0E2D200E2E210E2F1A0E2E2B0E2E2E.

Как перевести из одной системы в другую
На бумаге степень способа счисления обозначается нижним индексом после крайнего правого значения. В математике субскрипты используются нечасто в отличие от химии. Каждая формула содержит различные индексы нижнего и верхнего регистра.
Существует два способа осуществить перевод из двоичной системы в десятичную:
- позиционная нотация;
- удвоение.
Разбор перевода позиционной нотацией будет происходить на примере числа 10011011.
Первый шаг, чтобы произвести перевод числа из двоичной системы в десятичную - возведение всех чисел выражения в степень. Степень с каждым шагом увеличивается на 1, начинается с 0 справа налево. Выглядит это таким образом: 18 07 06 15 14 03 11 10. После преобразований получается числовой ряд 128, 64, 32, 16, 8, 4, 2, 1, сопоставляется с начальным 10011011.
Каждое число из возведенного в степень примера умножается на цифру примера 10011011 по порядку. Таким образом, 128 умножается на 1, 64 - на 0, 32 - на 0 и т.д. В итоге вычитаются все нулевые значения и остается 128, 16, 8, 2, 1. Для получения ответа в десятичной системе все цифры суммируются. Результат - 155.
Перевод методом удвоения проще для преобразования в уме или на бумаге. Этот способ перевода не использует математические функции со степенями, а только суммирование и простое умножение.
Способ подразумевает суммирование всех результатов, основываясь на многочлене a х 0 + b, где b равняется текущему значению, а - предыдущему. Эта функция применяется для каждого знака ряда 10011011. Для получения первого результата, следует исходить из утверждения, что предыдущее значение перед первой цифрой равняется 0. Следуя из этого, после подставления данных образовывается многочлен 0 х 2 + 1 и дает ответ - 1. Для второй цифры 0 получается многочлен 1 х 2 + 0, ответ - 2. Для третьего знака 0 - многочлен 2 х 2 + 0, ответ, соответственно, 4. Сумма равняется результату перевода в десятичной системе.
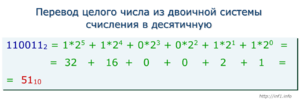
Как перевести число из десятичной системы в двоичную
Эта задача для перевода числовых знаков, так же как и предыдущая, имеет два варианта решения:
- вычитание и сравнение уменьшающихся степеней;
- сокращение с остатком.
Первый способ перевода подразумевает хорошее знание деления на 2. Особенностью способа является то, что при делении образовываются два возможные остатка - 0 и 1. Имено они и формируют числовое значение.
Чтобы перевести число 156 на язык машин, исполняются следующие правила. Для начала сумма делится на 2, что дает результат 78 с нулевым остатком. Первый остаток записывается в двоичное значение. Полученный результат делится снова на 2, что в итоге получается ответ 39 так же с нулевым остатком. Второй остаток записывается в следующий по порядку знак. Половина из числа 39 равняется 19 с остатком 1. После проведения всех операций получается число в двоичной системе - 00111001.
Второй способ формирует числовой ряд из результатов возведения цифры 2 до тех пор, пока это значение не станет больше, чем начальное. Получается последовательность 128, 64, 32, 16, 8, 4, 2, 1. Таким образом, судя по полученным знакам ряда, 156 делится на 128, дает единицу с остатком. Первая цифра в двоичном числе равняется 1. Далее происходит вычитание 128 из 156, что дает ответ 28. Число делится на следующий знак ряда. Таким образом, 26 делится на 64 и это дает 0 с остатком. Это следующее значение в двоичном коде. После проведения всех операций получаем целое двоичное число 00111001_2.

Заключение
Понимание правил, по которым происходит перевод чисел из одной системы в другую, - одно из базовых знаний программирования. Однако каждый раз переводить вручную числа или текст в машинный язык не потребуется. Сегодня существует множество онлайн-сервисов и десктопных приложений для таких целей. А основные значения по ходу работы запоминаются. При этом следует помнить, что глубокое понимание основ отличает начинающего программиста от профессионала.
Видео
Из этого видео вы узнаете, как выполнить перевод числа из двоичной в десятичную систему.